标准均值方差有效组合权重估计

均值-方差有效组合是给定期望收益，通过调整组合权重实现投资组合风险最小化，或给定 风险，通过调整组合权重实现投资组合收益最大化。该问题可以用数学表达式表示如下：

\[ w_{mvp}=\min_w w^\prime \Sigma w \\ s.t. wl=1 \\ w\mu=\bar{\mu} \]

其中，\(\Sigma\) 是投资组合中资产收益的协方差,\(l\)为所有元素为1得向量，\(\mu\)为股票收益向量，\(\bar{u}\)为投资组合期望收益。

该优化问题可以进一步表述为带有均值方差偏好和风险厌恶因子表达式,具体如下：

\[ w_{mvp}=\max_w w^\prime\mu- \frac{\gamma}{2} w^\prime\Sigma w \\ s.t. wl=1 \]

其中，\(\gamma\)为风险厌恶系数。

最优组合问题的解如下：

\[ w_{\gamma}^{*}=\frac{1}{\gamma}(\Sigma^{-1}-\frac{1}{l^{\prime}\Sigma^{-1}l}\Sigma^{-1}ll^{\prime}\Sigma^{-1})\mu+\frac{1}{l^{\prime}\Sigma^{-1}l}\Sigma^{-1}l \]

在实证中，估计该系数常常存在很多问题。例如，在短期内，\(\mu\)和\(\Sigma\)的估计有很大的噪声；甚至当资产的数量\(N\)超过收益率时间序列长度（\(T\)）时，收益率的方差协方差矩阵\(\Sigma\)将不再是正定矩阵，其逆矩阵将不存在。为了解决这个问题，一些正则化技术应用而生(Ledoit and Wolf 2004, 2003, 2004, 2012; Fan, Fan, and Lv 2008)。

考虑估计不确定性与交易成本的均值方差有效组合权重估计

由于资产收益噪声较大，估计的参数具有很强的不确定性，因此，在不确定性条件下估计参数将面临重大挑战，Wang (2005) 在模型和不确定性下对投资组合选择提供了理论分析；Pflug, Pichler, and Wozabal (2012) 证明了在所有资产上等权配置是对抗模型不确定性的最优选择。

在估计参数的不确定性中，交易成本是大家担心的主要问题，组合调整是有成本的，最优选择应该取决于投资者当前的持仓。在实证中，只给的收益率\(\hat{\mu}\)与其方差-协方差矩阵\(\hat{\Sigma}\)，得到的最优估计权重非常糟糕，文献提出了很多办法来克服该问题。例如，一种办法是对方差-协方差矩阵\(\hat{\Sigma}\)施加正则化，利用资产定价模型估计得到的先验信息(Kan and Zhou 2007)；或者使用高频数据来改善预测。

一个操作简便、有效（即使在高维度情况下）且纯粹受经济论据启发的统一框架是对交易成本进行事前调整(Hautsch and Voigt 2019)。假设资产收益来自于均值为\(\mu\)，方差与协方差矩阵为\(\Sigma\)的正太分布，并进一步假设组合调整的交易成本的函数形式如下：

\[ v(w_{t+1},w_{t+},\beta)=\frac{\beta}{2}(w_{t+1}-w_{t+})^\prime (w_{t+1}-w_{t+}) \]

其中，成本参数\(\beta>0\)，\(w_{t+1}=w_t \circ (1+r_t)/l^\prime (w_t \circ (1+r_t))\),\(w_{t+}\)代表组合调整前的权重。\(w_{t+1}\)与\(w_{t+}\)不同主要由上期收益造成。当组合权重从\(w_{t+}\)调整到\(w_{t+1}\)时，交易成本是对组合业绩的惩罚。

在以上设定中，交易成本不是线性增加的，组合调整越大，对组合收益影响越大。这时，投资者的组合最优化问题为：

\[ w_{mvp}=\max_w w^\prime\mu- v(w_{t+1},w_{t+},\beta)-\frac{\gamma}{2} w^\prime\Sigma w\\ =max_w w^\prime\mu^\star- \frac{\gamma}{2} w^\prime\Sigma^\star w\\ s.t. wl=1 \]

其中，\(\mu^\star=\mu+\beta w_{t+}\),\(\Sigma^\star=\Sigma+\frac{\beta}{\gamma}I\)

所以，交易成本的调整意味着一个带有收益参数调整（\(\mu^\star\),\(\Sigma^\star\)）的均值方差最优组合选择。求解的组合权重如下：

\[ w_{\gamma}^{*}=\frac{1}{\gamma}(\Sigma^{\star-1}-\frac{1}{l^{\prime}\Sigma^{\star-1}l}\Sigma^{\star-1}ll^{\prime}\Sigma^{\star-1})\mu+\frac{1}{l^{\prime}\Sigma^{\star-1}l}\Sigma^{\star-1}l \]

最优组合选择求解代码

我们考虑均值-方差最优组合权重求解的一般形式，beta为交易成本\(\beta\)（以调整前持有股票为条件），\(\beta=0\)为标准的均值-方差有效组合形式，gama为投资者的风险厌恶参数\(\gamma\)，w_pre为组合调整前的权重\(w_{t+}\)。计算组合权重的函数如下：

compute_efficient_weight <- function(Sigma,
                                     mu,
                                     gamma = 2,
                                     beta = 0, # transaction costs
                                     w_prev = rep(
                                       1 / ncol(Sigma),
                                       ncol(Sigma)
                                     )) {
  iota <- rep(1, ncol(Sigma))
  Sigma_processed <- Sigma + beta / gamma * diag(ncol(Sigma))
  mu_processed <- mu + beta * w_prev

  Sigma_inverse <- solve(Sigma_processed)

  w_mvp <- Sigma_inverse %*% iota
  w_mvp <- as.vector(w_mvp / sum(w_mvp))
  w_opt <- w_mvp + 1 / gamma *
    (Sigma_inverse - w_mvp %*% t(iota) %*% Sigma_inverse) %*%
      mu_processed
  
  return(as.vector(w_opt))
}

数据准备

pacman::p_load(tidyfinance,tidyverse,scales,tidyquant,mongolite,ggrepel,dplyr,zoo,ggplot2,nloptr)
url <- "mongodb://yingjie:19901225xyj@8.tcp.vip.cpolar.cn:14798/stockdata"
mb<-mongo(collection = "stockbase", db = "stockdata", url = url)
code<-mb$find()|>
  head(30)|>
  select(ts_code)|>
  pull()
m <- mongo(collection = "qfqtradedatadaily", db = "stockdata", url = url)
# 构造 MongoDB 查询符号（"$in" 语法）和日期范围
symbol_query <- paste(sprintf('"%s"', code), collapse = ", ")

query <- sprintf('{
  "ts_code": { "$in": [%s] },
  "trade_date":{"$gte":"20000101",
  "$lte":"20241231"}
}', symbol_query)

prices_daily<-m$find(query=query)|>
  mutate(trade_date=as.Date(trade_date,"%Y%m%d"))|>
  as_tibble()

##计算收益率

returns_daily <- prices_daily |>
  group_by(symbol) |>
  mutate(ret = close / lag(close) - 1) |>
  select(symbol, trade_date, ret) |>
  drop_na(ret)

returns_wide <- returns_daily |> 
  pivot_wider(names_from = symbol, values_from = ret) |> 
  na.omit()

sigma <- returns_wide |> 
  select(-trade_date) |> 
  cov()

计算最优权重

mu<-colMeans(returns_wide|>select(-trade_date))
w_efficient <- compute_efficient_weight(sigma, mu)
round(w_efficient, 3)

##  [1] -0.669  0.049  0.174  0.299 -0.249 -0.539  0.306 -0.076 -0.235  0.530
## [11]  0.508 -0.497  0.347  0.197  0.279 -0.249 -0.087 -0.041  0.735  0.238
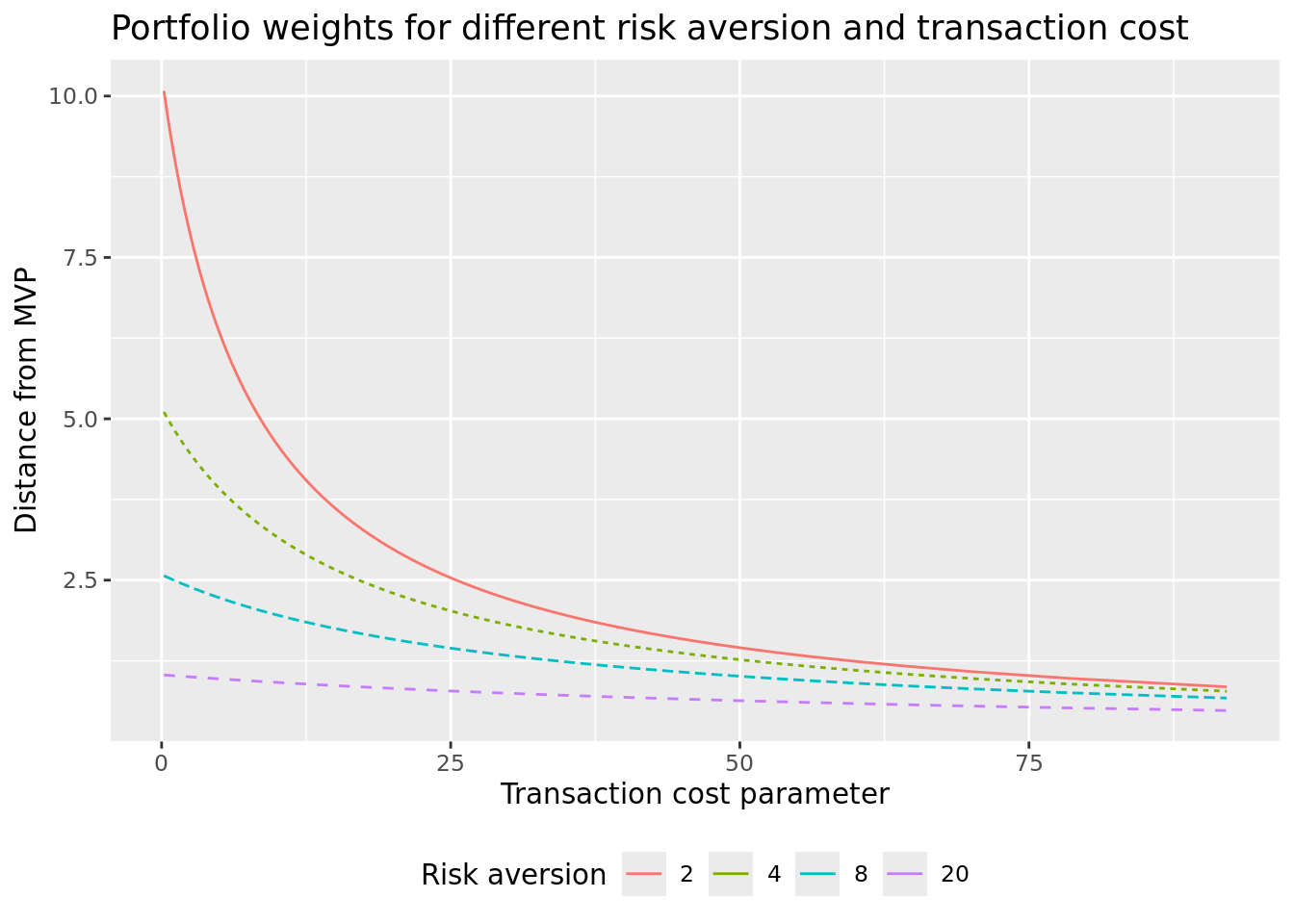
## [21]  0.594 -0.415 -0.110  0.284  0.034 -0.512  0.415 -0.053  0.815 -1.073

以上计算结果是交易成本为0，风险厌恶系数为2的情形，权重为负的意味着做空。那么，不同水平的交易成本和风险厌恶水平下，最优投资组合如何选择？下面将通过代码来说明该问题。

gammas <- c(2, 4, 8, 20)
betas <- 20 * qexp((1:99) / 100)
w_mvp <- solve(sigma) %*% rep(1, 30)
w_mvp <- as.vector(w_mvp / sum(w_mvp))                   
transaction_costs <- expand_grid(
  gamma = gammas,
  beta = betas
) |>
  mutate(
    weights = map2(
      gamma,
      beta,
      \(x, y) compute_efficient_weight(
        sigma,
        mu,
        gamma = x,
        beta = y / 10000,
        w_prev = w_mvp
      )
    ),
    concentration = map_dbl(weights, \(x) sum(abs(x - w_mvp)))
  )


transaction_costs |>
  mutate(risk_aversion = as_factor(gamma)) |>
  ggplot(aes(
    x = beta,
    y = concentration,
    color = risk_aversion,
    linetype = risk_aversion
  )) +
  geom_line() +
  guides(linetype = "none") + 
  labs(
    x = "Transaction cost parameter",
    y = "Distance from MVP",
    color = "Risk aversion",
    title = "Portfolio weights for different risk aversion and transaction cost"
  )+theme(
    legend.position = "bottom",            # 图例位置在底部
    legend.justification = "center",       # 图例居中
    legend.box.just = "center",            # 图例盒子居中
    legend.box = "horizontal"              # 图例方向水平排列
  )

均值-方差投资组合约束最优化求解

最长见的约束是卖空限制，这意味着负权重将不被允许（即\(w_i\ge0\)）。在最优过程中引入约束，我们可以通过数值最优化方法来求解组合权重。这需要使用 nloptr 包来求解最优权重，该包提供了数值优化方法的通用接口，特别地，我们使用了序列最小二乘程序（SLSOP）算法，该算法允许同时处理多个不等式约束的二阶可导的目标函数，要求提供优化的目标函数、目标函数对应梯度、约束条件及雅可比矩阵。

注意，near() 是一种用于成对比较两个向量是否相等的安全方法。相比之下，使用 == 对浮点数进行比较时对微小差异非常敏感，而这些差异可能是由于计算机中浮点数的表示方式造成的；而 near() 则内置了一个容差机制。

具体求解代码如下：

n_industries=30
w_initial <- rep(1 / n_industries, n_industries)

objective_mvp <- function(w) {
  0.5 * t(w) %*% sigma %*% w
}

gradient_mvp <- function(w) {
  sigma %*% w
}

equality_constraint <- function(w) {
  sum(w) - 1
}

jacobian_equality <- function(w) {
  rep(1, n_industries)
}

options <- list(
  "xtol_rel"=1e-20, 
  "algorithm" = "NLOPT_LD_SLSQP", 
  "maxeval" = 10000
)

w_mvp_numerical <- nloptr(
  x0 = w_initial, 
  eval_f = objective_mvp, 
  eval_grad_f = gradient_mvp,
  eval_g_eq = equality_constraint,
  eval_jac_g_eq = jacobian_equality,
  opts = options
)

all(near(w_mvp, w_mvp_numerical$solution))

## [1] TRUE

objective_efficient <- function(w) {
  2 * 0.5 * t(w) %*% sigma %*% w - sum((1 + mu) * w)
}

gradient_efficient <- function(w) {
  2 * sigma %*% w - (1 + mu)
}

w_efficient_numerical <- nloptr(
  x0 = w_initial, 
  eval_f = objective_efficient, 
  eval_grad_f = gradient_efficient,
  eval_g_eq = equality_constraint, 
  eval_jac_g_eq = jacobian_equality,
  opts = options
)

all(near(w_efficient, w_efficient_numerical$solution))

## [1] FALSE

上述结果表明，在我们已知解析解的情形下，数值方法确实成功地恢复了最优权重。对于更复杂的优化问题，R 的优化任务视图（optimization task view）提供了对广泛优化方法的概览。

接下来，我们将处理一些不存在解析解的问题。首先，我们加入空头卖出限制（short-sale constraints），这意味着需要引入不等式约束。我们可以通过设定一个下界向量 lb = rep(0, n_industries) 来实现空头卖出限制。接下来，我们将处理一些不存在解析解的问题。首先，我们加入空头卖出限制（short-sale constraints），这意味着需要引入不等式约束。我们可以通过设定一个下界向量 lb = rep(0, n_industries) 来实现空头卖出限制。

w_no_short_sale <- nloptr(
  x0 = w_initial, 
  eval_f = objective_efficient, 
  eval_grad_f = gradient_efficient,
  eval_g_eq = equality_constraint, 
  eval_jac_g_eq = jacobian_equality,
  lb = rep(0, n_industries),
  opts = options
)

round(w_no_short_sale$solution, 3)

##  [1] 0.000 0.000 0.000 0.000 0.000 0.000 0.066 0.000 0.000 0.198 0.040 0.000
## [13] 0.019 0.000 0.000 0.000 0.000 0.000 0.124 0.000 0.192 0.000 0.000 0.000
## [25] 0.000 0.000 0.000 0.000 0.361 0.000